bomo的开发随笔

记录工作学习点滴

0%

【OpenGL案例3】绘制金字塔、六边形、圆环

发表于 分类于

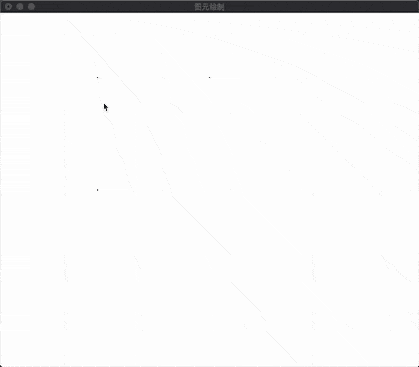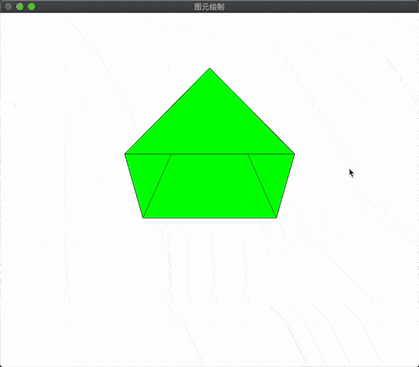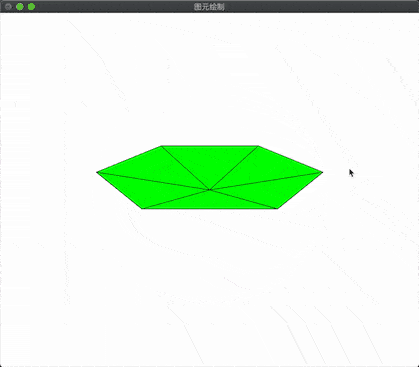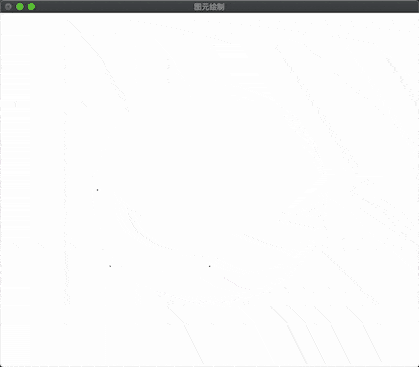
上节说到了不同的图元的装配方式，本节主要通过绘制金字塔，圆环，并使用透视投影，和矩阵变换来控制图形的显示

基础知识

OpenGL涉及到的基础变换主要有下面4种

变换 说明
视图变换 移动观察者的位置，观察者动，物体不动
模型变换 在场景中移动物体，观察者不动，物体动
投影变换 正投影，透视投影
视口变换 对窗口上最终输出进行缩放

其中对于同一个物体，使用视图变换和模型变换都能做到同样的效果，具体采用什么变换取决于实际情况

视图变换

视图变换是应用到场景中的第一种变换，通过物体/观察者在Z轴上的移动（默认是Z轴，也可以改为其他轴），确定场景中利于观察的位置。默认情况下，透视投影中的观察者位置处于原点（0，0，0），并沿着z轴负方向看向屏幕里面，一般通过moveForward方法来调整观察者位置，moveForward默认的朝向是-z轴，所以向屏幕里面移动传正数值，向屏幕外即+z轴，需要传负数值

1
2
3
4
5
6
7
8
9
// 定义一个参考证
GLFrame                cameraFrame;

// 向屏幕外（+z轴方向）移动15.0f
cameraFrame.MoveForward(-15.0f);

// 生成矩阵到mCamera，用于矩阵变换操作
M3DMatrix44f mCamera;
cameraFrame.GetCameraMatrix(mCamera);

模型变换

模型变换，主要涉及三个函数，移动、旋转、缩放。有了这三个函数的组合，我们可以进行任意变换。

1
2
3
4
5
6
7
8
9
10
11
// 平移，沿x/y/z三个方向平移，矩阵结果放在第一个参数里面
void m3dTranslationMatrix44(M3DMatrix44f m, float x, float y, float z);

// 旋转
void m3dRotationMatrix44(M3DMatrix44f m, float angle, float x, float y, float z);

// 缩放
void m3dScaleMatrix44(M3DMatrix44f m, float xScale, float yScale, float zScale);

// 矩阵叉乘，结果放在product
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b);

翻转操作可以用旋转，也可以用缩放（缩放到-1）

投影变换

通常也在窗口改变的时候设置

1
2
3
4
5
6
GLFrustum              viewFrustum;
// 设置透视投影
viewFrustum.SetPerspective(35.0f, float(w) / float(h), 1.0f, 500.0f);

// 加载投影矩阵到矩阵堆栈projectionMatrix
projectionMatrix.LoadMatrix(viewFrustum.GetProjectionMatrix());

视口变换

视口变换相关函数为，通常在窗口大小改变的时候修改

1
2
// 修改glView视口
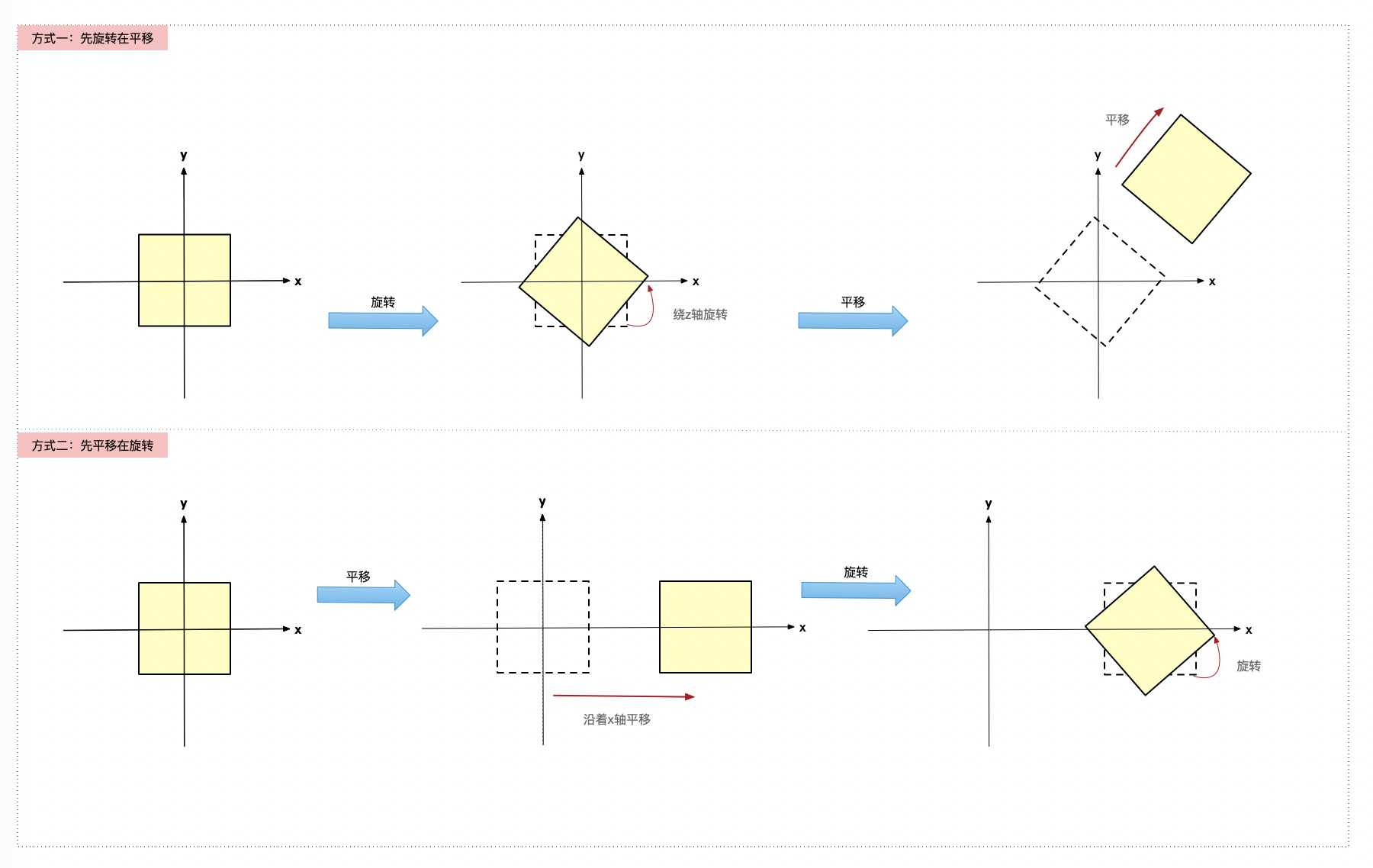
glViewport (GLint x, GLint y, GLsizei width, GLsizei height);

这里需要注意的是，矩阵变换叉乘不满足交换律，变换顺序会导致结果不一致

绘制

定义7个批次类，用于保存顶点

1
2
3
4
5
6
7
GLBatch                pointBatch;
GLBatch                lineBatch;
GLBatch                lineStripBatch;
GLBatch                lineLoopBatch;
GLBatch                triangleBatch;
GLBatch                triangleStripBatch;
GLBatch                triangleFanBatch;

在setupRC初始化顶点数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
// 定义三个点
GLfloat vCoast[] = {
    3,3,0,
    0,3,0,
    3,0,0
};

// 画点
pointBatch.Begin(GL_POINTS, 3);
pointBatch.CopyVertexData3f(vCoast);
pointBatch.End();

// 画线
lineBatch.Begin(GL_LINES, 3);
lineBatch.CopyVertexData3f(vCoast);
lineBatch.End();

// 画连续线段
lineStripBatch.Begin(GL_LINE_STRIP, 3);
lineStripBatch.CopyVertexData3f(vCoast);
lineStripBatch.End();

// 画闭合线段
lineLoopBatch.Begin(GL_LINE_LOOP, 3);
lineLoopBatch.CopyVertexData3f(vCoast);
lineLoopBatch.End();

// 3个三角形，构成金字塔形状
GLfloat vPyramid[12][3] = {
    -2.0f, 0.0f, -2.0f,
    2.0f, 0.0f, -2.0f,
    0.0f, 4.0f, 0.0f,

    2.0f, 0.0f, -2.0f,
    2.0f, 0.0f, 2.0f,
    0.0f, 4.0f, 0.0f,

    2.0f, 0.0f, 2.0f,
    -2.0f, 0.0f, 2.0f,
    0.0f, 4.0f, 0.0f,

    -2.0f, 0.0f, 2.0f,
    -2.0f, 0.0f, -2.0f,
    0.0f, 4.0f, 0.0f
};
triangleBatch.Begin(GL_TRIANGLES, 12);
triangleBatch.CopyVertexData3f(vPyramid);
triangleBatch.End();

// 三角形扇形--六边形
GLfloat vPoints[100][3];
int nVerts = 0;
// 半径
GLfloat r = 3.0f;
// 原点(x,y,z) = (0,0,0);
vPoints[nVerts][0] = 0.0f;
vPoints[nVerts][1] = 0.0f;
vPoints[nVerts][2] = 0.0f;

// M3D_2PI 就是2Pi 的意思，就一个圆的意思。 绘制圆形
for (GLfloat angle = 0; angle < M3D_2PI; angle += M3D_2PI / 6.0f) {
    // 数组下标自增（每自增1次就表示一个顶点）
    nVerts++;
    /*
        弧长=半径*角度,这里的角度是弧度制,不是平时的角度制
        既然知道了cos值,那么角度=arccos,求一个反三角函数就行了
        */
    // x点坐标 cos(angle) * 半径
    vPoints[nVerts][0] = float(cos(angle)) * r;
    // y点坐标 sin(angle) * 半径
    vPoints[nVerts][1] = float(sin(angle)) * r;
    // z点的坐标
    vPoints[nVerts][2] = -0.5f;
}

// 结束扇形 前面一共绘制7个顶点（包括圆心）
// 添加闭合的终点
// 课程添加演示：屏蔽177-180行代码，并把绘制节点改为7.则三角形扇形是无法闭合的。
nVerts++;
vPoints[nVerts][0] = r;
vPoints[nVerts][1] = 0;
vPoints[nVerts][2] = 0.0f;

// 加载！GL_TRIANGLE_FAN 以一个圆心为中心呈扇形排列，共用相邻顶点的一组三角形
triangleFanBatch.Begin(GL_TRIANGLE_FAN, 8);
triangleFanBatch.CopyVertexData3f(vPoints);
triangleFanBatch.End();

// 三角形条带，一个小环或圆柱段
// 顶点下标
int iCounter = 0;
// 半径
GLfloat radius = 3.0f;
// 从0度~360度，以0.3弧度为步长
for (GLfloat angle = 0.0f; angle <= (2.0f*M3D_PI); angle += 0.3f) {
    //或许圆形的顶点的X,Y
    GLfloat x = radius * sin(angle);
    GLfloat y = radius * cos(angle);

    //绘制2个三角形（他们的x,y顶点一样，只是z点不一样）
    vPoints[iCounter][0] = x;
    vPoints[iCounter][1] = y;
    vPoints[iCounter][2] = -0.5;
    iCounter++;

    vPoints[iCounter][0] = x;
    vPoints[iCounter][1] = y;
    vPoints[iCounter][2] = 0.5;
    iCounter++;
}

//结束循环，在循环位置生成2个三角形
vPoints[iCounter][0] = vPoints[0][0];
vPoints[iCounter][1] = vPoints[0][1];
vPoints[iCounter][2] = -0.5;
iCounter++;

vPoints[iCounter][0] = vPoints[1][0];
vPoints[iCounter][1] = vPoints[1][1];
vPoints[iCounter][2] = 0.5;
iCounter++;

// GL_TRIANGLE_STRIP 共用一个条带（strip）上的顶点的一组三角形
triangleStripBatch.Begin(GL_TRIANGLE_STRIP, iCounter);
triangleStripBatch.CopyVertexData3f(vPoints);
triangleStripBatch.End();

然后在renderSence里面，把对应的批次类draw出来就可以了

1
2
3
4
5
6
7
8
9
// 画点
glPointSize(4.0f);
pointBatch.Draw();
glPointSize(1.0f);

// 画三角形
glLineWidth(2.0f);
lineLoopBatch.Draw();
glLineWidth(1.0f);

矩阵堆栈

本案例涉及到3个矩阵，视图矩阵（修改观察者位置），模型矩阵（旋转），投影矩阵（透视投影）

这里我们定义两个矩阵堆栈，来计算

1
2
3
4
5
// 矩阵堆栈，用于设置投影矩阵
GLMatrixStack          projectionMatrix;

// 矩阵堆栈，用于设置视图矩阵，模型矩阵，
GLMatrixStack          modelViewMatrix;

为了方便计算，我们定义一个变换管道transformPipeline，用于合并2个矩阵堆栈（投影矩阵堆栈projectionMatrix和模型视图矩阵堆栈modelViewMatrix）

1
2
3
4
5
// 几何变换的管道
GLGeometryTransform    transformPipeline;

// 设置变换管线以使用两个矩阵堆栈
transformPipeline.SetMatrixStacks(modelViewMatrix, projectionMatrix);

对于投影矩阵，直接在changeSize的时候配置就可以

1
2
3
4
5
6
7
// 透视投影
GLFrustum              viewFrustum;

// 设置透视投影
viewFrustum.SetPerspective(35.0f, float(w) / float(h), 1.0f, 500.0f);
// 重新加载投影矩阵到矩阵堆栈projectionMatrix
projectionMatrix.LoadMatrix(viewFrustum.GetProjectionMatrix());

接下来我们在renderSence配置模型视图矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 加载一个单元矩阵到栈顶
modelViewMatrix.LoadIdentity();

// 复制一份栈顶矩阵到栈顶
modelViewMatrix.PushMatrix();

// 获得视图矩阵
M3DMatrix44f mCamera;
cameraFrame.GetCameraMatrix(mCamera);

// 与栈顶矩阵叉乘并覆盖栈顶矩阵
modelViewMatrix.MultMatrix(mCamera);

// 获得模型矩阵
M3DMatrix44f mObjectFrame;
objectFrame.GetMatrix(mObjectFrame);

// 与栈顶矩阵叉乘并覆盖栈顶矩阵
modelViewMatrix.MultMatrix(mObjectFrame);

最终通过变换管道，生成矩阵传递给着色器

1
2
3
4
5
// 生成最终的矩阵
M3DMatrix44f *fMatrix = transformPipeline.GetModelViewProjectionMatrix()

// 传给平面着色器处理，vBlack为填充颜色
shaderManager.UseStockShader(GLT_SHADER_FLAT, fMatrix, vBlack);

对于几何图形除了直接填充颜色，还需要绘制边框（glPolygonMode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 开启多边形偏移
glPolygonOffset(-1.0f, -1.0f);
glEnable(GL_POLYGON_OFFSET_LINE);

// 开启反锯齿
glEnable(GL_LINE_SMOOTH);

// 开启混合
glEnable(GL_BLEND);
// 混合方法
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

// 绘制线框几何黑色版 三种模式，实心，边框，点，可以作用在正面，背面，或者两面
//通过调用glPolygonMode将多边形正面或者背面设为线框模式，实现线框渲染
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
//设置线条宽度
glLineWidth(2.5f);

shaderManager.UseStockShader(GLT_SHADER_FLAT, transformPipeline.GetModelViewProjectionMatrix(), vBlack);
pBatch->Draw();

// 复原原本的设置
//通过调用glPolygonMode将多边形正面或者背面设为全部填充模式
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
glDisable(GL_POLYGON_OFFSET_LINE);
glLineWidth(1.0f);
glDisable(GL_BLEND);
glDisable(GL_LINE_SMOOTH);

关于矩阵堆栈的操作

矩阵堆栈API 说明
GLMatrixStack::LoadIdentity(void) 在栈顶加载/覆盖一个单元矩阵
GLMatrixStack::LoadMatrix(const M3DMatrix44f m) 在栈顶加载/覆盖成矩阵m
GLMatrixStack::MultMatrix(const M3DMatrix44f m) 矩阵m与栈顶矩阵叉乘，结果覆盖栈顶矩阵
GLMatrixStack::GetMatrix(void) 获取栈顶矩阵
GLMatrixStack::PushMatrix(void) 拷贝栈顶矩阵入栈
GLMatrixStack::PushMatrix(const M3DMatrix44f m) 把矩阵m入栈
GLMatrixStack::PopMatrix(void) 出栈，移出栈顶矩阵

完整代码在这里